[Algorithm] C++ Topology Sort (위상정렬)

📚 Computer Science/Algorithm

[Algorithm] C++ Topology Sort (위상정렬)

스쳐가는비 2022. 9. 27. 16:15

위상 정렬

사이클이 없는 방향 그래프의 모든 노드를 방향성에 맞게 순서대로 나열하는것
예시) 학과목을 고려한 학습 순서 설정

출처 - https://www.youtube.com/watch?v=xeSz3pROPS8&list=PLVsNizTWUw7H9_of5YCB0FmsSc-K44y81&index=36

위 사진의 세 과목을 모두 듣기 위한 적절한 학습 순서는??

자료구조 - 알고리즘 - 고급 알고리즘 (O)
자료구조 - 고급알고리즘 - 알고리즘 (X)

진입차수와 진출차수

진입차수 (Indegree) : 특정한 노드로 들어오는 간선의 개수
진출차수 (Outdegree) : 특정한 노드에서 나가는 간선의 개수

위상 정렬 알고리즘

큐를 이용하는 위상 정렬 알고리즘 동작 과정은 다음과 같다.

진입차수가 0인 모든 노드를 큐에 넣는다.
큐가 빌 때까지 다음의 과정을 반복한다.
큐에서 원소를 꺼내어 해당 노드에서 나가는 간선을 그래프에서 제거한다.
새롭게 진입차수가 0이 된 노드를 큐에 넣는다.

예시

필수적으로 위상정렬을 수행할 그래프는 어느 한 부분이라도 순환 되면 안된다.

[초기 단계] 초기 단계에서는 진입차수가 0인 모든 노드를 큐에 넣는다. 즉 처음 노드가 큐에 삽입된다.

[Step 1] 큐에서 노드 1을 꺼낸 뒤에 노드 1에서 나가는 간선을 제거합니다.
이후 새롭게 진입차수가 0이 된 노드들을 큐에 삽입합니다.

[Step 2] 큐에서 노드 2를 꺼낸 후 노드 2에서 나가는 간선을 제거합니다.
마찬가지로 새롭게 진입차수가 0이 된 노드들을 큐에 삽입합니다.

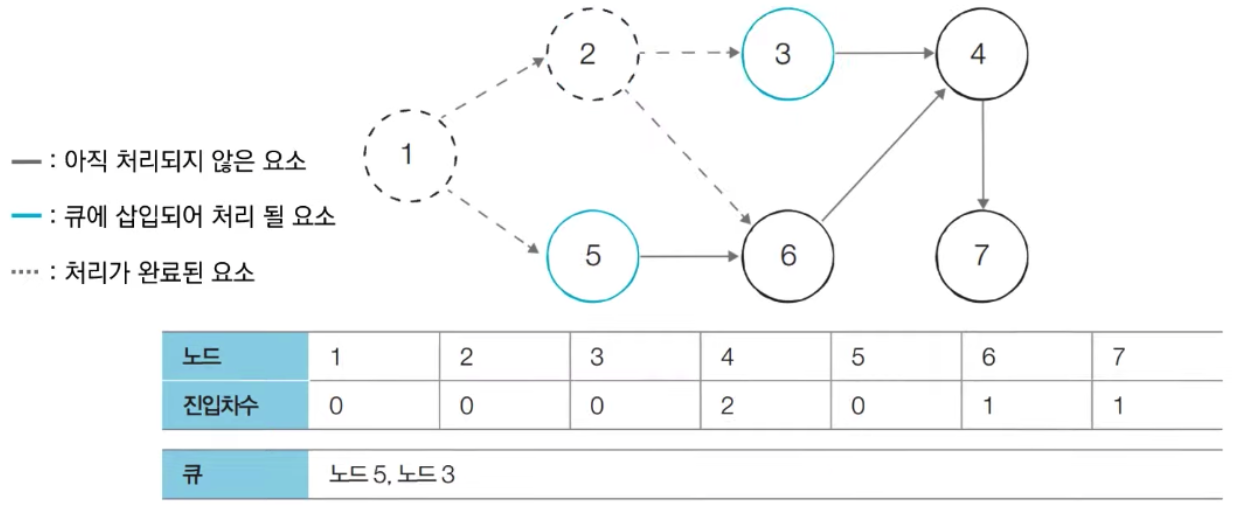
[Step 3] 큐에서 노드 5를 꺼낸 뒤에 노드 5에서 나가는 간선을 제거합니다.
새롭게 진입차수가 0이 된 노드들을 큐에 삽입합니다.

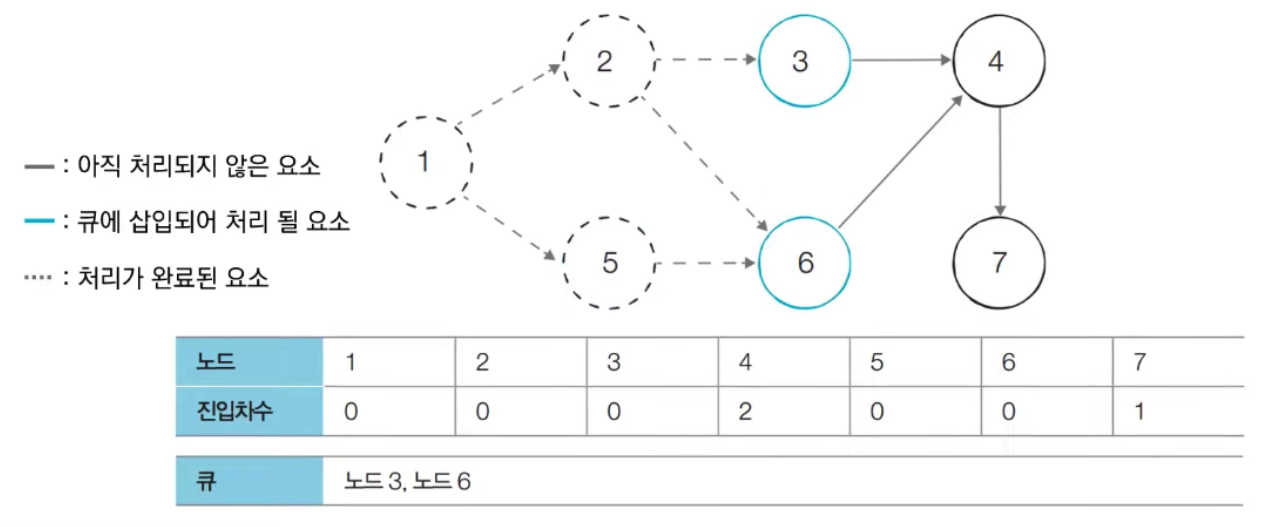
[Step 4] 큐에서 노드 3를 꺼낸 뒤에 노드 3에서 나가는 간선을 제거합니다.
새롭게 진입차수가 0이 된 노드들을 큐에 삽입합니다.

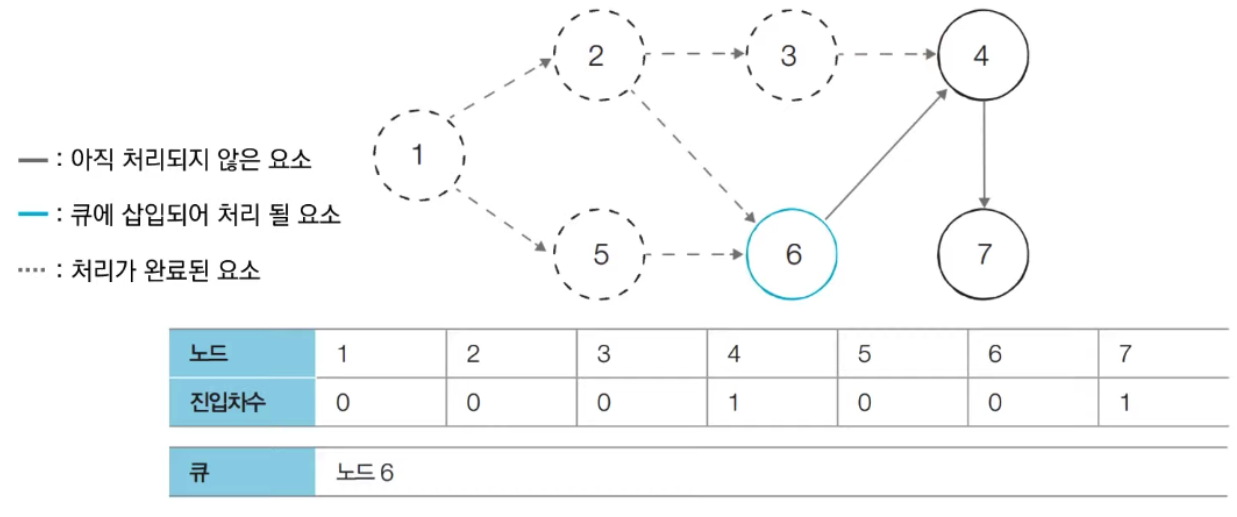
[Step 5] 큐에서 노드 6를 꺼낸 뒤에 노드 6에서 나가는 간선을 제거합니다.
새롭게 진입차수가 0이 된 노드들을 큐에 삽입합니다.

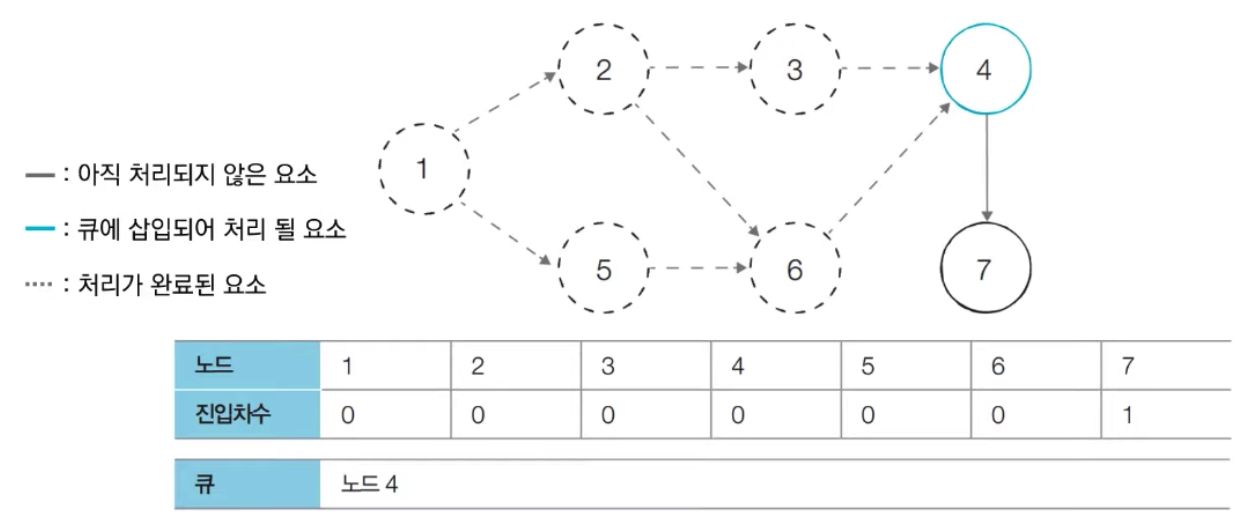
[Step 6] 큐에서 노드 4를 꺼낸 뒤에 노드 4에서 나가는 간선을 제거합니다.
새롭게 진입차수가 0이 된 노드들을 큐에 삽입합니다.

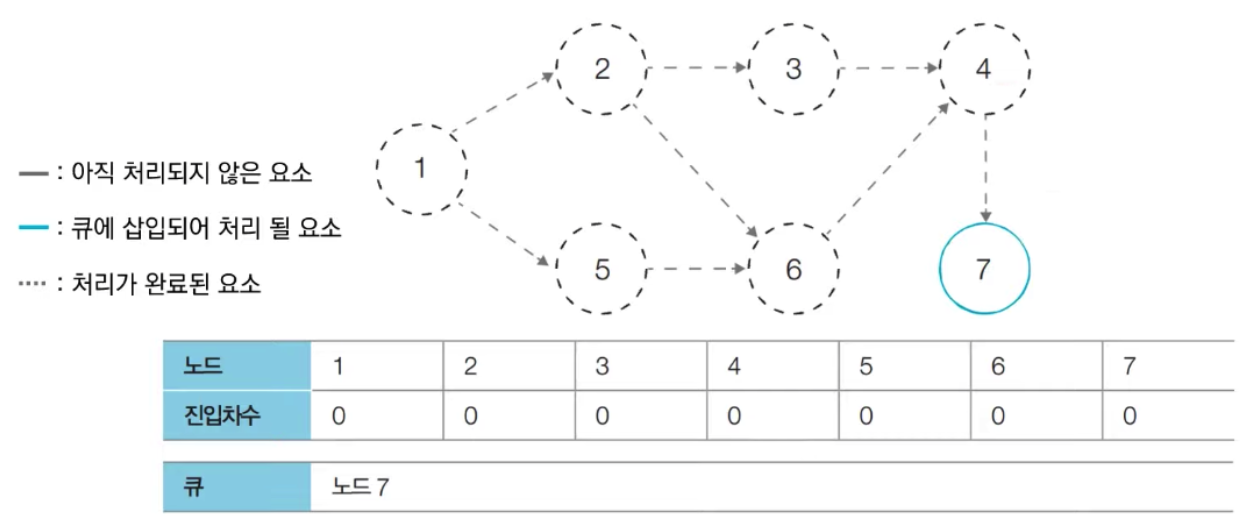
[Step 7] 큐에서 노드 7를 꺼낸 뒤에 노드 7에서 나가는 간선을 제거합니다.
새롭게 진입차수가 0이 된 노드들을 큐에 삽입합니다.

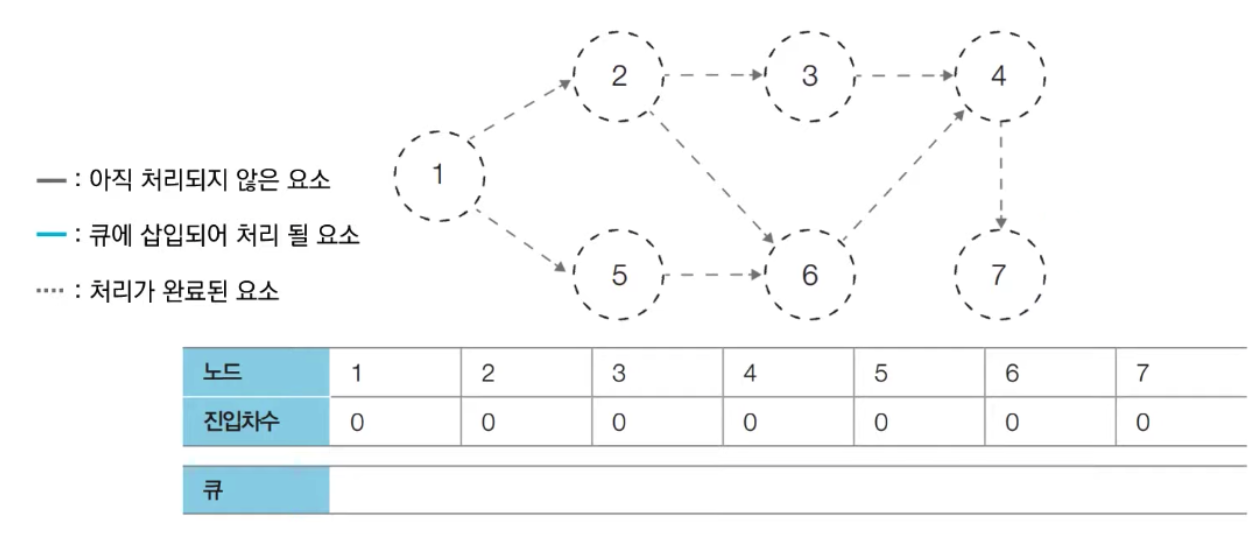
[결과]

큐에 삽입된 전체 노드 순서 : 1 - 2 - 5 - 3 - 6 - 4 - 7

위상 정렬의 특징

위상 정렬은 DAG에 대해서만 수행할 수 있다.
- DAG (Direct Acyclic Graph): 순환하지 않는 방향 그래프.
위상 정렬에서는 여러 가지 답이 존재할 수 있다.
- 한 단계에서 큐에 새롭게 들어가는 원소가 2개 이상인 경우가 있다면 여러 가지 답이 존재한다.
모든 원소를 방문하기 전에 큐가 빈다면 사이클이 존재한다고 판단할 수 있다.
- 사이클에 포함된 원소 중에서 어떠한 원소도 큐에 들어가지 못한다.
스택을 활용한 DFS를 이용해 위상 정렬을 수행할 수도 있다.

Code ( C++ )

#include <iostream>
#include <vector>
#include <queue>

using namespace std;

// Node 개수
#define NODECOUNT 7	

// 진입 차수 
int inDegree[NODECOUNT + 1];	

// 모든 Node의 Edge 정보
vector<int> Nodes[NODECOUNT + 1]; 

void topologySort() {
	// 위상정렬을 수행한 Node 순서 결과
	int sortedNode[NODECOUNT + 1];
	queue<int> Q;

	// 진입 차수가 0인 Node를 Queue에 모두 추가
	for (int i = 1; i <= NODECOUNT; i++) {
		if (inDegree[i] == 0) {
			Q.push(i);
		}
	}

	// 모든 Node 방문하여 간선이 없을 때까지 순서화된 Node 결과를 얻음
	for (int i = 1; i <= NODECOUNT; i++) {
		// N개의 모든 노드를 방문하기 전에 Queue가 empty이면 cycle이 발생함을 의미
		if (Q.empty()) {
			cout << "there may be a cycle node" << endl;
			return;
		}

		int x = Q.front();
		Q.pop();
		sortedNode[i] = x;

		// 연결이 되어있는 모든 정점들을 확인하면서 간선제거 
		for (int j = 0; j < Nodes[x].size(); j++) {
			int y = Nodes[x][j];

			// 진입차수가 '0'인 노드 큐에 추가
			if (--inDegree[y] == 0) {
				Q.push(y);
			}
		}
	}

	for (int i = 1; i <= NODECOUNT; i++) {
		cout << "Ordered Node:" << sortedNode[i] << endl;

		Nodes[i].clear();
	}

}

void addEdge(int start, int end)
{
	// Edge 연결, 방향성을 갖음
	Nodes[start].push_back(end);

	// 진입 차수 증가
	inDegree[end]++;
}

void solve()
{
	addEdge(1, 2);
	addEdge(1, 5);
	addEdge(2, 3);
	addEdge(2, 6);
	addEdge(3, 4);
	addEdge(4, 7);
	addEdge(5, 6);
	addEdge(6, 4);

	topologySort();
}

int main()
{
	solve();
	return 0;
}

티스토리

[Algorithm] C++ Topology Sort (위상정렬)

[Algorithm] C++ Topology Sort (위상정렬)

위상 정렬

진입차수와 진출차수

위상 정렬 알고리즘

예시

위상 정렬의 특징

관련 알고리즘 문제

Code ( C++ )